一、首先说明:
- 这是啥? —— 这是利用C#FORM写的一个用来演示计算机图形学中 ①Bresenham直线扫描算法(即:连点成线);②种子填充法(即:填充多边形);③扫描线填充法
- 有啥用? —— 无论是连点成线还是区域填充在高级编程中基本上都提供很高效的库函数来调用。这里拿出这些算法一方面有利于大家理解那些封装的函数底层是实现;另一方面是方便嵌入式TFT屏幕底层驱动开发时借鉴的。
- 是啥样? —— 如下面的操作,不言而喻。
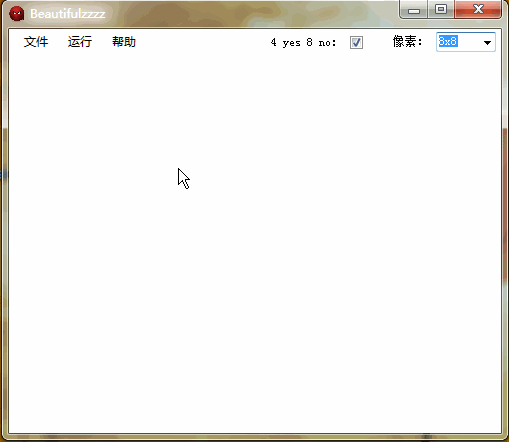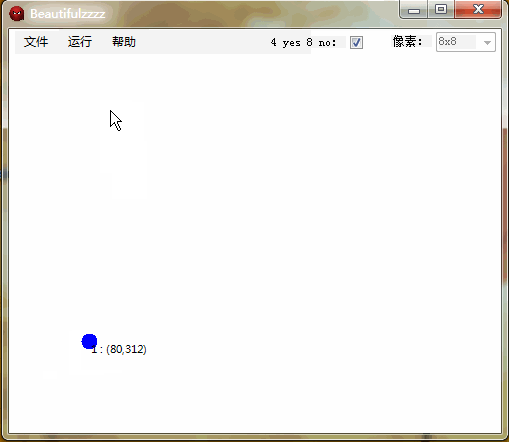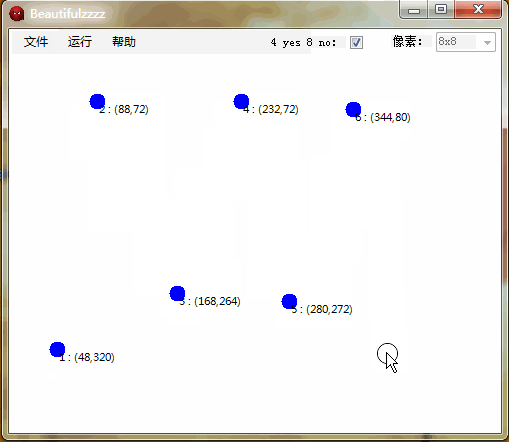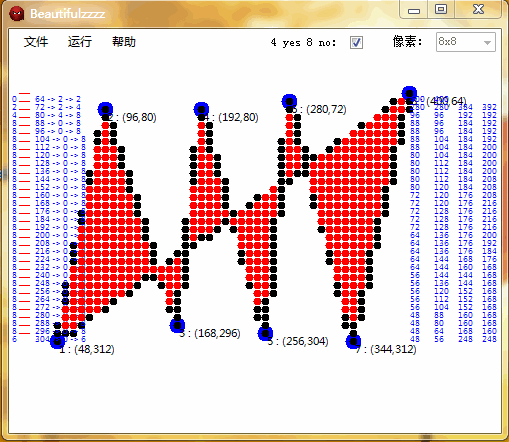
二、进入正题:
2-1、直线的扫描转换
图形的扫描转换实质就是在光栅等数字设备上确定一个最佳逼近于图形的像素集的过程。

对于直线扫描转换其实就是确定最佳逼近于该直线的一组像素,然后按照扫描线的顺序对这些像素进行写操作。三种比较常用的算法是:①数值微分法(DDA);②中点画线法;③Bresenham算法。这里主要讲第三个算法,因为这个效率高且易于硬件实现。
Bresenham算法:由于显示直线的象素点只能取整数值坐标,可以假设直线上第i个象素点坐标为(xi,yi) ,它是直线上点(xi,yi)的最佳近似,并且xi=xi(假设m<1),如下图所示。那么,直线上下一个象素点的可能位置是(xi+1,yi) 或(xi+1,yi+1)。
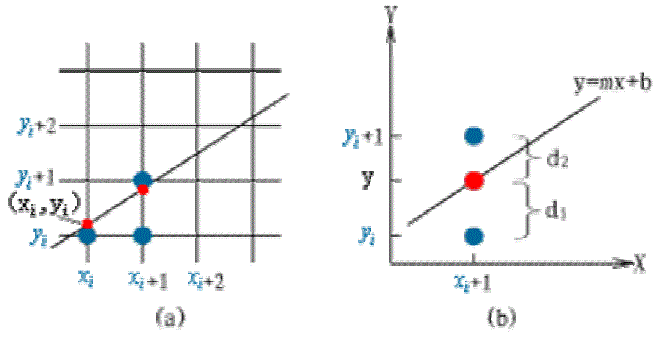
而实际的点为红色的点,可以计算可能点与实际点的偏差的差,即:d1-d2=2m(xi+1)-2yi+ 2b-1。这样根据这个差就能判断下一点的坐标,然后一直向前推进就能求出所有的点。此外由于考虑硬件对浮点数处理的速度要比对整数处理的速度慢许多的情况,在该算法里会对该式子做一些变换(其实就是放大使其变为整数,同时保证下一点求法正确)。由于网上资料很多,这里就不细讲了~
Bresenham算法伪代码:[条件:0<=m<=1且x1<x2]
①输入线段的两个端点坐标和画线颜色:x1,y1,x2,y2,color; ②设置象素坐标初值:x=x1,y=y1; ③设置初始误差判别值:p=2·Δy-Δx; ④分别计算:Δx=x2-x1、Δy=y2-y1; ⑤循环实现直线的生成:
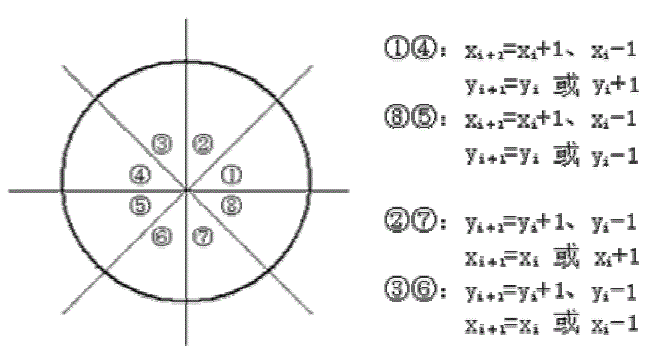
1 for(x=x1;x<=x2;x++) 2 { 3 putpixel(x,y,color); 4 if(p>=0) 5 { 6 y=y+1; 7 p=p+2*(Δy-Δx); 8 } 9 else10 { 11 p=p+2*Δy;12 }13 } 显然,上述算法是带有一定限制条件的,下面我们将其推广到所有斜率的情况,实现各种线的绘制。容易证明:当线段处于①、④、⑧、⑤区域时,以|Δx|和|Δy|代替前面公式中的Δx和Δy;当线段处于②、③、⑥、⑦区域时,把|Δx|和|Δy|对换。下面是工程中用于连点成线的基于Bresenham算法的函数:
1 ///2 /// Bresenham画线算法,给出两个点a,b 3 /// 4 /// PS:这里XiangSu是光栅的最小距离,因为我是在高分辨率的窗口中模拟低分辨率效果, 5 /// 所以用这个XiangSu来控制模拟的光栅最小单元格的边的大小,实际运用中XiangSu=1 6 /// 7 /// 8 void Bresenhamline(Point a, Point b) 9 {10 int x, y, dx, dy, s1, s2, p, temp, interchange, i;11 x = a.X;12 y = a.Y;13 dx = Math.Abs(b.X - a.X);14 dy = Math.Abs(b.Y - a.Y);15 if (b.X > a.X)16 s1 = XiangSu;17 else18 s1 = -XiangSu;19 if (b.Y > a.Y)20 s2 = XiangSu;21 else22 s2 = -XiangSu;23 if (dy > dx)24 {25 temp = dx;26 dx = dy;27 dy = temp;28 interchange = 1;29 }30 else31 interchange = 0;32 p = 2 * dy - dx;33 for (i = 1; i <= dx; i += XiangSu)34 {35 tempp.X = x;36 tempp.Y = y;37 tempP.Add(tempp);38 Vram[x + y * 600] = true;//把该片内存置为边界标记39 if (p >= 0)40 {41 if (interchange == 0)42 y = y + s2;43 else44 x = x + s1;45 p = p - 2 * dx;46 }47 if (interchange == 0)48 x = x + s1;49 else50 y = y + s2;51 p = p + 2 * dy;52 }53 }
由于版面受限,请链接到第二节,更加精彩,哈哈:
两篇链接:
[计算机图形学] 基于C#窗口的Bresenham直线扫描算法、种子填充法、扫描线填充法模拟软件设计(一)
本文转自beautifulzzzz博客园博客,原文链接:http://www.cnblogs.com/zjutlitao/p/4116783.html,如需转载请自行联系原作者